


In this article, I will demonstrate spatial clustering to identify clusters within an unordered point set based on expectation maximization of Gaussian distribution curves that represent each cluster around its median. This is a form of representative-based clustering in that it forms clusters of convex polygons around chosen center points.
Useful terms:
The algorithm consists of three steps: iteration, assignment, maximize.
Iteration A new set of representatives are calculated by iterating the current representatives. There is a 10% chance of assigning a new randomly chosen point as a representative, a 10% chance of removing an existing representative and a 80% chance of reassigning an existing representative as another randomly chosen point. If the set is currently empty, then a random point is chosen to be the first representative.
Assignment In this set, each point is assigned to the nearest representative as to form a convex polygon around it. If this is the first time it's called then there's only one representative (randomly selected), so all points are assigned to it as one cluster.
Maximize The overall cost of the clustered sets is calculated as the sum of the cost of each set. Due to using an inverse Gaussian distribtion, points further away from the cluster's center cost more. If the cost of the cluster set of the new representatives is higher than the previous set, these new representatives are kept for the next iteration, otherwise they are discarded. The aim is to maximize by minimizing the overall cost of the clusters by assigning points low on the Gaussian distribution for a cluster to another cluster where they are higher up and cost less. The steepness of the Gaussian distribution (determined by a single parameter) determines the optimal size of clusters within a set,
Clustering algorithm The algorithm terminates after either a fixed number of iterations or when it converges to 0 when the cost of all clusters are below a minimum threshold, whichever comes first. Within a few seconds, the algorithm can converge on a set of 5,000 points. If it continues running for another minute (when given an unusually high number of iterations), the overall improvement in clustering is less than 1%. There is no risk of early termination due to the Gaussian distribution and random selection of new representatives as opposed to shifting them towards cluster centroids from previous iterations.
 | |
| Gaussian distributions with different variances. Since the inverse is taken, higher values give smaller and tighter clusters while smaller values give larger clusters. | |
 |
 |
| As shown in the fitness function (lower is better, to minimize cluster cost), the cost of a cluster increases as the number of points within the cluster increase, but it increases faster when the cluster has a larger variance in distribution. The Gaussian distribution is scaled down in these images, fitness rises exponentially as it increases. | |
Results
 |
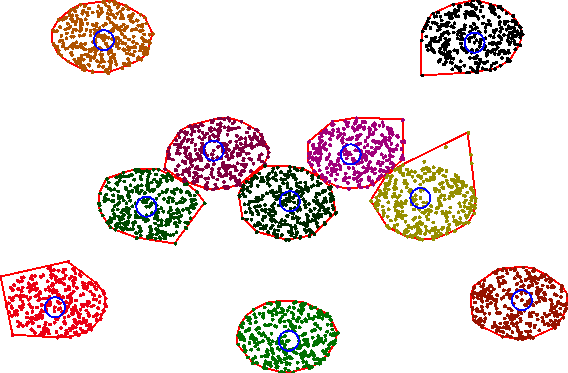 |
| A test dataset with a few outliers to confuse the solver. | 10 circles are correctly located and clustered with the default settings. |
Future improvements
#include "Clustering.h"
#include <sstream>
#include <fstream>
using namespace std;
// Scale depending on the units used
// Increase for smaller, tighter clusters
// Decrease for larger clusters
float gaussian_d_scale = 1.0f;
// Keep the solver under control
float threshold = 0.0001f;
void Clustering::FromFile(const char* filename)
{
points.clear();
delete[] dist_table;
delete[] expf_table;
CSVReader r(filename);
for (int iline = 0; iline < r.NumLines(); iline++)
{
ClusterPt pt;
r.GetLine(iline) >> pt.x >> pt.y;
points.push_back(pt);
}
dist_table = new float[points.size() * points.size()];
expf_table = new float[points.size() * points.size()];
int dsize = points.size();
for (int i = 0; i < dsize; i++)
{
for (int j = i + 1; j < dsize; j++)
{
float dx = points[i].x - points[j].x;
float dy = points[i].y - points[j].y;
float d = dx * dx + dy * dy;
expf_table[(i * dsize) + j] = expf_table[(j * dsize) + i] = expf(gaussian_d_scale * d / 2.0f);
d = sqrtf(d);
dist_table[(i * dsize) + j] = dist_table[(j * dsize) + i] = d;
}
}
}
void Clustering::ToFile(const char* filename)
{
std::ofstream of(filename);
for (int i = 0; i < points.size(); i++)
{
of << points[i].x << ',' << points[i].y << ',' << points[i].clusterID << endl;
}
of << "representatives";
for (int i = 0; i < representative_set.size(); i++)
{
of << ' ' << representative_set[i];
}
of << endl;
of.flush();
of.close();
}
std::vector<int> Clustering::NextReps(std::vector<int> reps)
{
vector<int> nreps = reps;
if (reps.empty()) { nreps.push_back(rand() % points.size()); }
else
{
int rnd = rand() % 10;
if (rnd == 0) { nreps.push_back(rand() % points.size()); }
else if (rnd == 1 && nreps.size() > 1) { nreps.erase(nreps.begin() + rand() % nreps.size()); }
else
{
nreps[rand() % reps.size()] = rand() % points.size();
}
}
return nreps;
}
void Clustering::AssignReps(std::vector<int>& reps, float OutliersThreshold)
{
int num_points = points.size();
int num_reps = reps.size();
int* rep_row = &reps[0];
for (int i = 0; i < num_points - 4; i += 4)
{
__m128 closestdist = _mm_set_ps(0, 0, 0, 0);
int closest_rep[4] = { -1, -1, -1, -1 };
for (int j = 0; j < num_reps; ++j)
{
int offset = i + (rep_row[j] * num_points);
__m128 ds = _mm_set_ps(dist_table[offset],
dist_table[offset + 1],
dist_table[offset + 2],
dist_table[offset + 3]);
int cmpmask = _mm_movemask_ps(_mm_cmplt_ps(ds, closestdist));
if (closest_rep[0] == -1)
{
closest_rep[0] = closest_rep[1] = closest_rep[2] = closest_rep[3] = j;
closestdist = ds;
}
else if (cmpmask)
{
if (cmpmask & (1 << 0)) { closest_rep[3] = j; }
if (cmpmask & (1 << 1)) { closest_rep[2] = j; }
if (cmpmask & (1 << 2)) { closest_rep[1] = j; }
if (cmpmask & (1 << 3)) { closest_rep[0] = j; }
closestdist = _mm_min_ps(closestdist, ds);
}
}
points[i + 0].clusterID = closest_rep[0];
points[i + 1].clusterID = closest_rep[1];
points[i + 2].clusterID = closest_rep[2];
points[i + 3].clusterID = closest_rep[3];
}
for (int i = num_points - 4; i < num_points; ++i)
{
int closest_rep = -1;
float closest_dist = 0;
int dist_row = (i * num_points);
for (int j = 0; j < num_reps; ++j)
{
float& d = dist_table[dist_row + rep_row[j]];
if (d < closest_dist || closest_rep == -1)
{
closest_rep = j;
closest_dist = d;
}
}
points[i].clusterID = closest_rep;
}
}
float Clustering::ClusterFitness(std::vector<ClusterPt>& points, std::vector<int>& reps, int clusterID)
{
int num_points = points.size();
float fit_sum = 0;
float fit_sumsq = 0;
float fitsize = 0;
float fit_gaussian = 0;
for (int i = 0; i < num_points; ++i)
{
Clustering::ClusterPt& pt = points[i];
if (pt.clusterID != clusterID) { continue; }
fit_gaussian += expf_table[(i * num_points) + reps[pt.clusterID]];
++fitsize;
}
if (fitsize < threshold) { return 0; }
float t = ((fit_gaussian * fit_gaussian) / (fitsize * fitsize)) - threshold;
return t > 0 ? t : 0;
}
float Clustering::Fitness(std::vector<Clustering::ClusterPt>& points, std::vector<int>& reps)
{
int num_points = points.size();
int max_cluster = -1;
for (int i = 0; i < num_points; ++i)
{
max_cluster = std::max(max_cluster, points[i].clusterID);
}
if (max_cluster == -1) { return 0; }
max_cluster++;
float fitness = 0;
for (int i = 0; i < max_cluster; i++)
{
fitness += ClusterFitness(points, reps, i);
}
return fitness;
}
void Clustering::Run()
{
std::vector<int> reps;
reps = NextReps(reps);
float prevfitness = -1;
int iterations = 0;
for (; iterations < 10000; iterations++)
{
vector<int> nreps = NextReps(reps);
AssignReps(nreps, outlier_threshold);
float newfitness = Fitness(points, nreps);
if (newfitness < prevfitness || prevfitness < 0)
{
reps = nreps;
prevfitness = newfitness;
cout << prevfitness << ' ' << reps.size() << endl;
}
if (newfitness < threshold) { break; }
}
AssignReps(reps, outlier_threshold);
cout << "Fitness: " << Fitness(points, reps) << ", iterations: " << iterations << endl;
representative_set = reps;
}